Na física, quando se estuda os fenômenos, avalia-se e mede-se as grandezas físicas. Elas devem transmitir as informações de modo completo para quem as utiliza. Ouve-se rotineiramente nos serviços de meteorologia as informações sobre a temperatura: “Amanhã no Rio fará 42ºC”. Quem assiste ao boletim consegue imaginar que o dia será de muito “calor”. Também ouve-se muito de motoristas em que o carro quebrou na rua: “ … empurrei ele para cima da calçada. Fiz bastante força...” Quem só ouve isso pode imaginar de diversas formas a cena, o motorista atrás do carro empurrando para frente, na frente empurrando para trás ou na lateral, manobrando ao volante e empurrando ao mesmo tempo. Ou seja, o ouvinte, só com as informações fornecidas, não tem como imaginar de imediato a forma que se desenrolou a cena. O motorista fez força1 e informou que “ fez bastante força, informou a magnitude da força. Mas quem ouve perguntará onde ele estava empurrando. Assim o motorista terá que informar mais um dado. Desta maneira percebe-se que a força só pode ser bem interpretada se for fornecido mais de uma informação. Para ser mais correto, três informações, pois ele empurra, mas poderia puxar também.
Assim na física as grandezas que necessitam três informações para ser bem entendida são chamadas de GRANDEZAS VETORIAIS, em oposição àquelas que necessitam somente de uma informação e que são chamadas de GRANDEZAS ESCALARES.
As duas grandezas físicas, escalares e vetoriais são representadas por entes matemáticos chamados de ESCALAR e VETOR, respectivamente. Uma terceira grandeza física chamada TENSORIAL e representada por TENSORES é uma expansão do conceito de vetor. Esta terceira grandeza necessita de 9 informações para ser ber definida ( 9 escalares ou 3 vetores)
Um escalar indica a intensidade da grandeza (módulo), a unidade de medida da grandeza representada e, nos casos em que os valores da grandeza podem assumir números negativos, sinal. Eles também seguem as regras e propriedades da álgebra numérica.
Um vetor contém três informações em uma única representação. Estas informações são:
módulo (intensidade): valor numérico da grandeza;
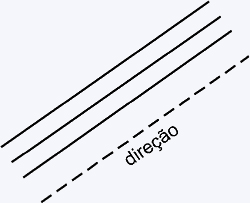
direção: é a característica que um feixe de retas paralelas tem em comum, representada na Figura 1.1-a
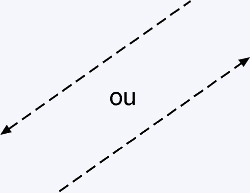
Sentido: é o lado, numa direção que a grandeza está sendo aplicada, mostrado na figura Figura 1.1-b
| a)
|
b)
|
| Figura 1.1: Representação Gráfica da direção e sentido. Em A) Retas de mesma direção (paralelas) e em B) vetores de sentidos opostos. | |
Um vetor é um ente matemático representado graficamente por um SEGMENTO ORIENTADO DE RETA (seta ou flecha), mostrado na figura . O vetor começa no ponto A, chamada de origem e termina no ponto B, chamada de ponta, formando o segmento orientado AB com orientação de A para B. Ele possui um nome representado por uma letra e uma seta acima desta. A letra e a seta devem ser interpretados como um único símbolo, indicando que o elemento se trata de um vetor. Esta representação é mostrada na Figura 1.2-a. Outras formas também são utilizadas, mostradas na Figura 1.2-b. A forma com acento circunflexo é utilizada para representar um versor (vetor unitário). Quando a letra parece sem a seta, ela deve ser interpretada como sendo somente o módulo do vetor.
|
a) |
b) |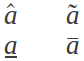
 |
 |
|
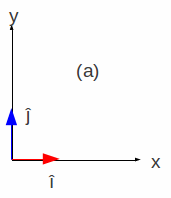
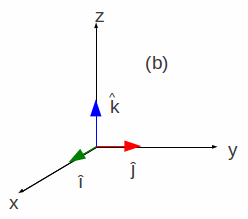
| Figura 1.2: Representação Gráfica da direção e sentido. Em A) Retas de mesma direção (paralelas) e em B) vetores de sentidos opostos. | Figura 1.3: Eixos definidos e seus respectivos versores. (a) em 2D e (b) em 3D. | |||
O módulo do vetor é representado pelo comprimento do segmento de reta. Num gráfico em escala, o tamanho representa fielmente a grandeza real que pode ser mensurada pela medida do tamanho do segmento com o auxilio de uma régua. Por exemplo, num gráfico de forças em que a escala seja 1:100 ( 1 cm para 100 N), um vetor que tenha o tamanho de 2 cm representa uma força de 200 newton2 Por outro lado, em gráficos sem escala, o tamanho do segmento é apenas uma indicação qualitativa, vetores grandes indicam grandezas de valore maiores, vetores de tamanho menor, grandezas de valores menor. Assim o módulo é representado junto ao vetor pelo seu nome sem o sinal da seta acima deste.
A direção é representada de diversas formas, a mais simples usa-se as pontos cardeais, por exemplo, direções Norte-Sul, Leste-Oeste, Nordeste-Sudoeste, etc. Outra forma matematicamente mais rigorosa é a utilização do círculo trigonométrico e uma direção referencial. A direção é definida pelo ângulo3 formado pela reta direcional e o eixo referencial.
Num sistema de coordenadas definidos pelos eixos direcionais e seus respectivos vetores unitários (versores)4, conforme a Figura 1.3, em (a) em duas dimensões (2D) (a) e em três dimensões (3D):
onde as relações são:
|
|
(1.1) |
O vetor pode ser representado pelo par de coordenadas na forma (x ; y) ou por uma expressão algébrica utilizando os vetores unitários:
|
|
(1.2) |
As coordenadas podem ser obtidas dos pontos que formam o vetor, onde as coordenadas do vetor são:
|
|
(1.3) |
Uma outra forma de representar os vetores é utilizando a notação matricial. Nesta as equações (1.2) ficam:
|
|
(1.4) |
Um vetor só é igual a outro se, e somente se os módulos, as direções e os sentidos forem iguais. A Figura 1.4 mostra casos onde os vetores não são iguais. No caso a, eles são diferentes pois os módulos são diferentes, no b, eles são diferentes pois, mesmo tendo mesmo tamanho (módulo) e direção (paralelos), tem sentidos diferentes. E no caso c eles são diferentes, pois tem direções diferentes. Pode-se comparar sentidos de vetores de mesma direção, em vetores de direções diferentes não tem significado comparar os sentidos.
 |
 |
 |
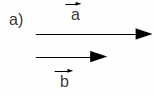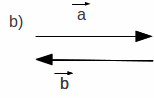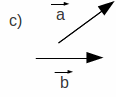| Figura 1.4: Desigualdade de vetores. Os vetores são desiguais em a) pelo módulo; em b) pelo sentido e em c) pela direção. | ||
Na Figura 1.5 tem-se três exemplos de pares de vetores iguais. Em todos os três exemplos, tanto os módulos como as direções e os sentidos são iguais.
a)
 |
|
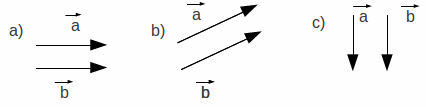| Figura 1.5: Exemplos de igualdade de vetores. | |
As operações com vetores não seguem as mesmas regras da álgebra
de escalares, pois além do módulo, tem-se que considerar a direções
e sentidos dos membros na operação. A operação com vetores é
realizada, de forma mais simples, em duas etapas. A primeira etapa é
a “operação gráfica”, após faz-se a operação algébrica.. A
segunda etapa pode ser desconsiderada em gráficos com escala de
valores, mas não nos gráficos sem escalas (qualitativos). Estas
duas etapas constituem um modo de resolução mais intuitivo. As
operações também podem ser realizadas com os vetores escritos na
forma cartesiana (eq.1.2).
Definindo dois vetores a e b, colineares representados na figura 1.6:
 |
|
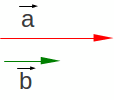Figura 1.6: Vetores colineares
|
A soma será dividida em quatro casos diferentes. Os três primeiros, em suma, são casos especiais do último, podendo ser calculados pelo último.
Vetores colineares são vetores que possuem mesma direção e
sentido. Definindo os vetores
e
,
conforme a Figura 1.6, cujos módulos são, respectivamente, a
e b. A operação:
|
|
(1.5) |
é, graficamente vista na Figura 1.7.
 |
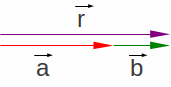Figura 1.7: Resultante
 (violeta)
da soma dos vetores (vermelho) e (verde). |
O procedimento é simples, Escolhe-se um dos dois vetores como primeira parcela5
, reproduz-se o escolhido num novo diagrama. O outro vetor (segunda parcela é
reproduzido de tal modo que seu ponto inicial coincida com o ponto final do
anterior. Se houver mais parcelas, redesenha-se cada uma da mesma maneira, ou
seja o ponto inicial de um vetor coincide com o ponto final do anterior6.
O vetor soma7
terá seu ponto inicial no ponto inicial do primeiro vetor parcela
colocado no diagrama e seu ponto final no ponto final do último
vetor parcela reproduzido. A Figura 1.7 mostra o vetor,
resultante da adição dee
,
mostrando a direção e o sentido e, percebe-se que o módulo do
vetor resultante, r é a soma algébrica dos módulos dos
vetores
e
,
ou seja:
|
|
(1.6) |
 |
|
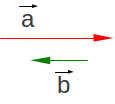Figura
1.8: Vetores antiparalelose
. |
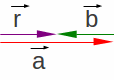
Vetores antiparalelos são vetores que possuem a mesma direção e
sentidos opostos. Definindo os vetorese
,
conforme a Figura 1.18, cujos módulos são, respectivamente, a
e b. A operação:
|
|
(1.7) |
é, graficamente vista na Figura 1.9.
 |
|
Figura
1.9: Resultante
(violeta)
da soma dos vetores
(vermelho)
e
(verde). |
O procedimento é idêntico ao anterior, reproduzindo o primeiro
vetor num novo diagrama, em seguida reproduzido o segundo vetor, com
seu ponto inicial coincidente ao ponto final do vetor anterior. O
vetor soma terá seu ponto inicial no ponto inicial do primeiro vetor
parcela colocado no diagrama e seu ponto final no ponto final do
último vetor parcela reproduzido, também como no anterior. A Figura
1.9 mostra o vetor
,
resultante da adição dee
,
mostrando a direção e o sentido e, percebe-se que o módulo do
vetor resultante, r é a subtração algébrica dos módulos
dos vetorese
,
ou seja:
|
|
(1.8) |
 |
|
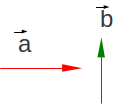Figura
1.10: Vetores perpendicularese
. |
Vetores perpendiculares são vetores formam um ângulo reto ( π rad ou 90º). Definindo os
vetorese
,
conforme a Figura 1.10, cujos módulos são, respectivamente, a
e b.
A operação:
|
|
(1.9) |
é, graficamente vista na Figura 1.11.
 |
|
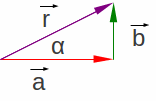Figura
1.11: Resultante
(violeta)
da adição dos vetores
(vermelho)
e
(verde). |
,
resultante da adição de
e
,
mostrando a direção e o sentido. A direção mostrada é tal que a
reta que a contém faz um ângulo α com a horizontal. Percebe-se
os vetores formam um triângulo. Devido ao cálculo do módulo de
ser
escalar, pode-se utilizar somente os módulos dos vetorese
,
como mostrado na Figura 1.12. O módulo do vetor resultante
se
relaciona com os vetores parcelas de acordo com o Teorema de
Pitágoras. Ou seja:|
|
(1.10) |
 |
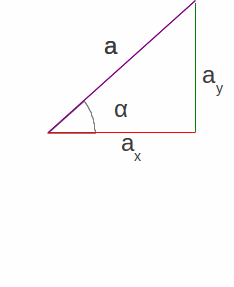Figura 1.12: Figuras geométricas formadas pelos módulos dos vetores parcelas e soma. |
O ângulo α é calculado a partir da função trigonométrica tangente definida a partir dos triângulos retângulos, que é:
|
|
(1.11) |
que para o triângulo da Figura acima resulta:
|
|
(1.12) |
Assim calculando o ângulo direcional.
 |
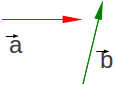| Figura
1.13: Vetores quaisquere
que
tem um ângulo θ entre si.
|
Este caso de adição é o mais geral. Todos os três anteriores
podem ser resolvidos poe esta maneira. Definindo os vetorese
,que
fazer entre si um ângulo θ
conforme a Figura 1.13, cujos módulos são, respectivamente, a
e b.
A operação:
|
|
(1.13) |
é graficamente vista na Figura 1.14.
 |
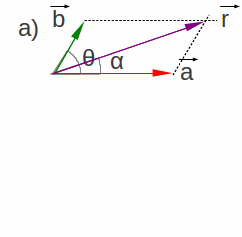Figura
1.14: Resultante(violeta)
da soma dos vetores
(vermelho)
e(verde).
Em a) a adição pela regra do paralelogramo e, em b) pela regra do
triângulo. |
 |
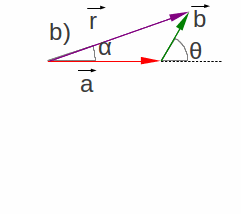A nela vê-se o vetor
,
resultante da adição dee
,
sua direção (ângulo α)
e o sentido. Na Figura 1.14-a a adição é mostrada pela regra do
paralelogramo8
O módulo do vetor resultante, r deve ser calculado com o
auxílio da lei dos cossenos adaptada ao ângulo θ e aos módulos, como no triângulo
formado na Figura 1.14, ou seja::
|
|
(1.14) |
Se os vetorese
estiverem
na forma algébrica (eq. 1.2):
|
|
(1.15) |
A adição
é:
|
|
(1.16) |
que é válida para qualquer soma. Nesta maneira de escrever o vetor, o módulo:
|
|
(1.17) |
e o ângulo de
inclinação de
com
a horizontal é:
|
|
(1.18) |
Na álgebra de escalares, utiliza-se regras de sinal para simplificar a expressão:
|
|
(1.19) |
onde a operação de adição se transformou numa operação de subtração. De modo inverso se houver uma subtração, pode-se convertê-la numa adição, conforme a seguinte passagem:
|
|
(1.20) |
A mesma lógica é utilizada na álgebra vetorial, ou seja, a operação:
|
|
(1.21) |
é transformada numa adição de modo que:
|
|
(1.22) |
de modo que os
operadores da adição são, agora,
e
.
Este segundo vetor é definido a partir de.
O sinal altera o sentido do vetor, se modo a permanecer inalterados
módulo e direção. Se o vetor
é
definido conforme a Figura 1.13, o vetor
é:
 |
Figura 1.15: Definição de
a partir de
 . |
Desta forma a subtração9 se torna um caso da adição e um dos quatro casos de adição deve ser utilizado para a resolução. A resolução então desta adição tem como resultado exatamente o valor da subtração.
A multiplicação de vetores se divide em três casos. Nos dois primeiros casos os operadores são vetores e no terceiro um é vetor e o outro é um valor escalar (numérico).
O produto escalar ou interno é a operação entre dois vetores que resulta num escalar.
Definindo dois vetores:
|
|
(1.23) |
o produto escalar
entre
e
é:
|
|
(1.24) |
Pode-se interpretar o produto escalar como o módulo da projeção do
vetor
na
direção do vetor
.
que é mostrado geometricamente na Figura 1.16 em 2D.
 |
Figura
1.16: Projeção de
na direção de
.
Definição geométrica do produto escalar em 2D. A distância
demarcada pela linha azul corresponde ao resultado do produto
escalar. |
No produto escalar, são válidas as propriedades:
|
|
(1.25) |
Também temos o produto escalar definido pelos módulos dos vetores e o ângulo formado por eles:
|
|
(1.26) |
Esta definição para produto escalar, resulta numa nova definição para cosseno de um ângulo:
|
|
(1.27) |
1.3.3.2
Produto vetorial ou produto externo
O produto vetorial ou produto externo é a operação com vetores que
resulta num vetor perpendicular aos operadores. Definindo dois
vetores
e
conforme
Figura 1.17:
|
|
Figura 1.17: vetor resultante
do produto vetorial entre
e
.
Na figura a esquerda, a disposição espacial dos vetores; e na
direita a regra da mão direita aplicada ao produto vetorial. |
.
Também pode-se definir os vetores algebricamente conforme (1.23)
que, e o produto vetorial dee
é:
|
|
(1.28) |
uma forma compacta.
O módulo do vetor resultante do produto vetorial pode ser calculado utilizando a relação algébrica:
|
|
(1.29) |
O produto vetorial possui as seguintes propriedades:
|
|
(1.30) |
e a área do polígono formado pelos vetores, como na Figura 1.18, é dada também pelo módulo do produto vetorial, ou seja:
|
|
(1.31) |
 |
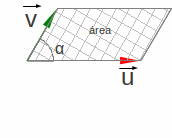Figura 1.18: Polígono formado pelos vetorese
. |
Definindo o vetor
de
módulo g, de acordo com a Figura 1.19:
Figura 1.19: Vetor a.
e o escalar a, o
vetor
,
resultante de:
|
|
(1.32) |
será um vetor de módulo igual a:
|
|
(1.33) |
direção igual a do
vetor
e
sentido, conforme a Figura 1.20-a, igual a
se
a > 0 e oposto a
,
conforme a Figura 1.20-b, se a < 0:
a)  |
b)
 |
| Figura 1.20: Vetor
resultante f do produto a
|
|
A decomposição na matemática é a operação que encontra um conjunto de elementos que operados resultam no valor a ser decomposto e que segue algumas regras pré-definidas. Por exemplo a decomposição por fatores primos. A operação sobre os elementos é a multiplicação e só pode-se incluir números primos. Desta maneira decompondo o valor 120 em fatores primos, através de divisões sucessivas de quociente inteiro e resto nulo, pelos primos de menor valor possível:
|
|
(1.34) |
Assim pode-se reescrever 120 por fatores primos:
|
|
(1.35) |
A mesma lógica é empregada na decomposição de vetores. Sendo que o vetor é formado por parcelas, a quantidade destas depende da quantidade de dimensões envolvidas,. por exemplo: duas dimensões (2D), duas parcelas, três dimensões (3D), três parcelas, etc10. A soma das parcelas, obrigatoriamente será:
|
|
(1.36) |
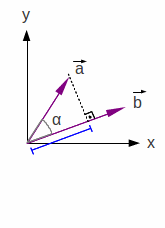
Definindo o vetor
,
em 2D, conforme a Figura 1.21, deve-se escolher as duas parcelas
(
e
)
de tal modo que:
|
|
(1.37) |
 |
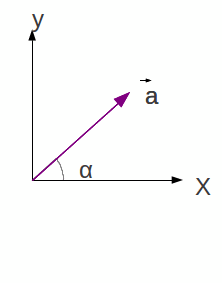Figura
1.21: Definição do vetor
a
que faz um ângulo com
a horizontal (eixo x).
|
Segue-se o procedimento a seguir:
 |
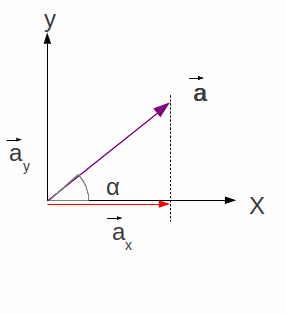Figura 1.22: Projeção do vetor
 no eixo x. |
Escolhe-se um dos eixos para iniciar;
traça-se uma reta paralela ao outro que passe na extremidade do vetor e que corte o eixo inicial;
o segmento de reta entre a origem e o ponto de corte define a
projeção do vetor
no
eixo x, o vetor
conforme
Figura 1.22.
traça-se uma reta paralela ao primeiro eixo que passe na extremidade do vetor e corte o eixo final;
o segmento de reta entre a origem e o ponto de corte define a
projeção do vetor
no
eixo y, o vetor
,
conforme Figura 1.23.
 |
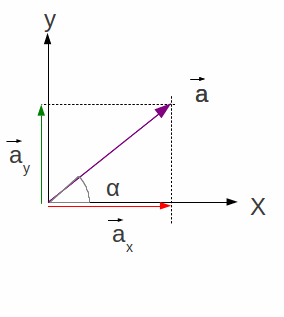Figura
1.23: Projeção do vetor
no
eixo y , vetor |
Se o gráfico estiver em escala, para se saber o módulo das
projeções, basta medi-las com uma régua e aplicar a escala para
saber o seu valor real. Por exemplo, se o vetor
representa
uma velocidade, suas projeções também representam velocidades em
cada eixo e o gráfico possuir escala de 1 cm : 10 m/s, cada cm
medido no gráfico equivale a uma velocidade de 100 m/s. Se a medida,
com a régua, de uma das distâncias for 5 cm, o vetor representará
50 m/s de módulo.
Percebe-se que se forma um retângulo entre os vetores projeçãoe,
as retas auxiliares e os eixos, onde a diagonal deste, o vetor
,
divide-o em dois triângulos retângulos iguais, representados na
Figura 1.24-a. Utilizar-se-á o triângulo de baixo11,
representado vetorialmente pela figura Figura 1.24-b ou escalarmente
pela Figura 1.24-c. No cálculo mais simplificado o utilização do
triângulo com os valores escalares se mostra mais útil. E desta
maneira que se inicia a etapa numérica.
 |
 |
 |
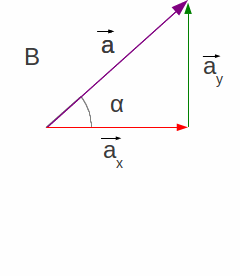
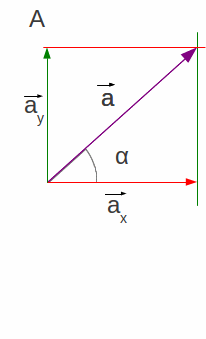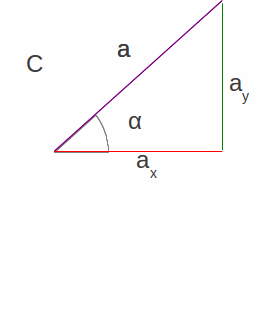| Figura 1.24: Figuras geométricas formadas pelos vetores, linhas auxiliares e eixos. Em a) o retângulo formado com os vetores, linhas auxiliares e eixos, em b) o triângulo inferior formado pelos vetores e, em c), o triangulo equivalente com a medida dos módulos. | ||
As funções trigonométricas definidas pelas relações em triângulos retângulos são:
|
|
(1.38) |
que equivalem, no triângulo da Figura 1.24-c, a seguinte relação:
|
|
(1.39) |
Aplicando as relações trigonométricas (1.38) considerando as relações (1.39) tem-se:
|
|
(1.40) |
ou na forma mais relevante:
|
|
(1.41) |
As expressões (1.41) fornecem os valores numéricos (módulos) dos
vetores projeção
e
1 A força será definida pelas leis de Newton.
2 Unidade de media de força que será definida pelas leis de Newton
3 Preferencialmente medir ângulos em radianos. Em alguns casos pode-se utilizar graus e frações decimais de graus.
4 Versor (vetor unitário) é um vetor que tem módulo 1 e indica as direções ortonormais que definem um espaço vetorial. Cada espaço, dentre os quais, o cartesiano (retangular), cilíndrico e esférico, possui um conjunto de versores diferentes. A relação entre versores de espaços diferentes será visto mais adiante.
5 A propriedades da adição de escalares são válidas para adição de vetores.
6 Como na adição de números, pode-se somar mais de dois vetores ao mesmo tempo. Desde que se siga as regras de reprodução dos vetores parcelas.
7 O vetor que resulta de uma operação de aritmética também é chamado de resultante. Este termo é bastante empregado na literatura em detrimento do nome das partes da operação.
8 A regra do paralelogramo utiliza os traços auxiliares paralelos aos vetores que passam pelo extremo do outro de modo a formar um paralelogramo. A origens dos vetores operandos replicados num novo gráfico devem estar no mesmo ponto. Na decomposição de vetores utiliza-se novamente este método.
9 As propriedades da subtração de escalares se aplica a subtração de vetores.
10 Em uma dimensão (1D) o vetor e a parcela serão absolutamente iguais.
11 O uso do triângulo superior levaria aos mesmos resultados finais. Os ângulos deste podem ser descobertos apenas utilizando a teoria de feixe de paralelas cortadas por uma reta transversal e o fato de que a soma dos ângulos internos do triângulo é igual a π rad (180º) .
12 A função “sin α” se refere a função seno α (sen α), No corpo do texto utiliza-se sen, mas nas expressões matemáticas aparece como “sin”.
.
.
.
;
.
.
.
.
;
.
;
;
;
;
.
;
;
;
.
.
.
.
;
.
;
.
;
;
.
.
.
.
;
.